Objetivos

Este objeto de aprendizagem apresenta atividades e fundamentos sobre a ordenação de dados, descrevendo em detalhes quatro métodos que podem ser utilizados nesta tarefa.

A ferramenta é indicada para estudantes de graduação, especialmente alunos da disciplina de algoritmos. O AMO pode ser usado como apoio para o ensino presencial por professores e alunos em sala de aula ou na realização de atividades extra classe.

• Público: Estudantes de graduação, especialmente alunos da disciplina de algoritmos. O AMO pode ser usado como apoio para o ensino presencial por professores e alunos em sala de aula ou na realização de atividades extra classe.
• Autores: Evandro Franzen, Maria Claudete Wildner, Mouriac Halen Diemer, Luis Antônio Schneiders.
• Assessoria técnica: Artur Welp

Situação problema:

O professor da disciplina de Algoritmos decide que a ordem de apresentação dos projetos finais, que representam a terceira nota do semestre, será por ordem crescente das datas de aniversário dos estudantes. Para tanto, entrega o conjunto de datas de aniversário dos estudantes regularmente matriculados nesta disciplina em uma estrutura de dados conhecida como vetor e decide que a própria turma encontre e aplique um método de ordenação deste vetor. Bem, embora os estudantes conheçam vetores e os pré-requisitos para a utilização dos mesmos, ainda não conhecem os métodos de ordenação destes, problema que decide resolver com a aplicação de um Objeto de Aprendizagem (OA) específico.

Resultado esperado:

É esperado que, com base no vetor recebido e com o apoio do Objeto de Aprendizagem para ordenação de vetores, os estudantes apresentem o vetor com as datas de aniversário ordenadas em ordem crescente para que este seja utilizado pelo professor na organização das apresentações dos projetos finais em sua disciplina de Algoritmos.

Para verificar os seus conhecimentos sobre o conteúdo básico de algoritmos, resolva o Desafio Inicial.

Se o seu score ficar abaixo de 70%, acesse e faça um bom estudo do material indicado abaixo:

• Wiki Livros - Introdução à programação/Algoritmos
• Introdução a Algoritmos e Programação Introdução a Algoritmos e Programação

Algoritmos de ordenação

Bubble sort

Um dos métodos de ordenação mais conhecidos é o Bubble Sort. Este algoritmo também é chamado de ordenação por flutuação ou bolha e é um dos que apresenta uma das menores complexidades. A lógica do algoritmo consiste em percorrer a lista diversas vezes, fazendo com que o menor elemento seja inserido no topo. O termo “bolha” diz respeito a esta ideia, ou seja, a bolha (menor elemento) deve “emergir” até chegar a superfície.

Neste algoritmos os elementos são comparados aos pares (o primeiro com o segundo, o segundo com o terceiro, o terceiro com o quarto, ...) em rodadas sucessivas, trocando suas posições sempre que necessário. Na primeira rodada o elemento maior acabará se posicionado na última posição, ou seja, na sua posição definitiva. Portanto, na rodada seguinte, o maior elemento já estará posicionado. Assim a cada rodada podemos reduzir uma comparação. Uma lista de n elementos estará ordenada depois de n-1 rodadas ou, antes disso, quando percebemos que ao final de uma rodada nenhuma troca ocorreu.

Acompanhe este exemplo:

Considere que é necessário ordenar a lista de números 10, 7, 3, 15, 9. Para ordenar esta lista de 5 elementos serão necessárias 4 rodadas de comparação. Iniciamos a primeira rodada comparando o número 10 e o 7 e trocamos suas posições, gerando a lista 7, 10, 3, 15, 9. Continuamos comparando agora o 10 com 3 e novamente trocamos suas posições, gerando a lista 7, 3, 10, 15, 9. Seguimos comparando o 10 com o 15 (sem trocar) e depois o número 15 com o número 9, trocando suas posições e gerando, ao final a primeira rodada a lista 7, 3, 10, 9, 15. Observe que o número 15 acabou posicionado ao final da lista.

Repete-se então todo o processo, pela segunda vez, considerando apenas os 4 primeiros elementos 7, 3, 10 e 9, pois o número 15 já está posicionado. No final desta rodada a lista será 3, 7, 9, 10, 15. Repete-se o processo considerando agora apenas os 3 primeiro elementos 3, 7 e 9, pois é sabido que os dois valores maiores já estão posicionados corretamente. Como não houve trocas nesta terceira rodada podemos interromper o processo, ou seja a quarta e última rodada não será necessária.

Abaixo observe as ilustrações do funcionamento do algoritmo.

Shell sort

Animação

Select sort

Animação

Insert sort

Neste algoritmo deve-se percorrer a sequência da esquerda para a direita, ou seja, em cada rodada elege-se um elemento para análise (inciando pela esquerda) e procura-se a posição em que ele deve ser inserido, sempre em comparação com seus anteriores. Ao descobrir a posição de inserção todos os elementos entre esta posição e a posição onde está o elemento eleito, são deslocados uma posição para direita, transferindo o elemento eleito para a posição de inserção.

Acompanhe este exemplo:

Considere que desejamos ordenar a sequência de números 3, 1, 4, 2, 7. Começamos elegendo o número 1 (que está na segunda posição), então comparamos o número 1 com os seus anteriores e percebemos que a posição correta dele é a primeira. Deslocamos então o número 3 uma casa para direita e o número 1 assume a posição inicial. A lista fica então 1, 3, 4, 2, 7. Elegemos agora o número 4 (que está na posição 3) e o comparamos com os seus anteriores. Percebemos que a posição dele não deve ser mudada, pois todos os anteriores são menores do que ele. Passamos então para o número 2 (que está na posição 4) e o comparamos com seus anteriores. A posição correta dele é a segunda, então deslocamos todos os elementos entre a segunda posição e a quarta posição uma casa para a direita e inserimos o número 2 na segunda posição. A lista fica então 1, 2, 3, 4, 7. Continuamos o processo agora elegendo o número 7 (que está na quinta posição). Comparamos o número 7 com seus anteriores e percebemos que não há necessidade de mudança. A lista estará ordenada quando atingirmos o último elemento, ou seja, esta lista encontra-se ordenada.

Abaixo observe a ilustração do funcionamento do algoritmo.

Guia

Ao clicar no botão iniciar você será direcionado à página inicial que irá descrever o problema da ordenação e na qual você irá realizar um desafio com questões sobre algoritmos e ordenação de dados. A realização da atividade é muito importante porque irá demonstrar a importância da ordenação de dados e também vai estimular a sua busca pelo conhecimento sobre os métodos descritos.

Após o desafio inicial você poderá continuar o seu caminho por este objeto, acessando informações sobre os seguintes métodos: Bubble sort, Shell sort, Select sort e Insert sort. Em cada uma das páginas que apresentam os métodos citados você encontrará textos, vídeos e uma atividade que contribuirá para que você compreenda os conceitos e o funcionamento dos algoritmos.

Mapa de navegação

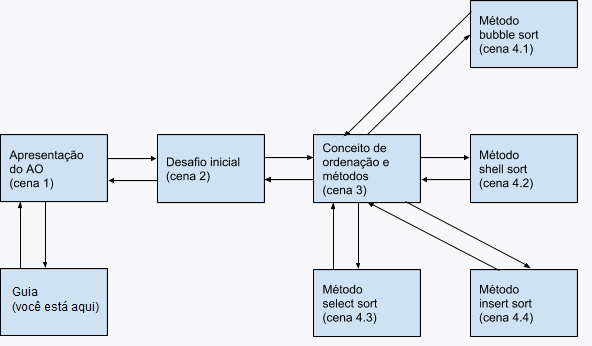
Vá em frente e bom aprendizado!

Créditos

Conteúdo e Desenvolvimento

Evandro Franzen

Maria Claudete Wildner

Mouriac Halen Diemer

Luis Antônio Schneiders

Revisão

Maria Elisabete Bersch

Assessoria técnica

Artur Welp